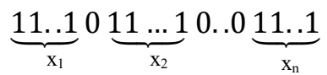Bài toán chia kẹo Euler là một bài toán tổ hợp xuất hiện từ nhiều năm về trước, Đây là một bài toán rất hay và có nhiều ứng dụng trong Toán học. xuất phát từ một vướng mắc rất đơn giản, nhà bác học Leohard Euler đã phát biểu nó thành một bài toán rất thú vị. Những kiến thức khác hoàn toàn so với những kiến thức THCS hay THPT như công thức nhân 3.

Bài toán mở đầu

“Có m chiếc kẹo giống nhau, cần chia chúng cho n em bé. Hỏi có bao nhiêu cách chia kẹo như vậy?”

Bài toán tưởng chừng như đơn giản, nhưng nó lại gây khó khăn cho không ít học sinh. Từ bài toán này, người ta đã phát triển ra cách giải cho vô số bài toán đếm khác nhau. trong bài viết này, tôi sẽ giới thiệu tới các bạn phương pháp giải bài toán chia kẹo Euler và một vài phần mềm từ cơ bản tới nâng cao của nó. Tất nhiên, nội dung các bài toán sẽ ảnh hưởng nhiều tới lập trình, do đó tôi sẽ bỏ qua những bài toán quá khó (mà chỉ dành cho học sinh chuyên Toán).

Phương pháp giải bài toán căn bản

Nếu như gọi số kẹo mà mỗi em bé nhận được lần lượt là 1,2,…, (0≤≤;∀:1≤≤)x1​,x2​,…,xn​ (0≤xi​≤m;∀i:1≤i≤n). Bài toán lúc đó sẽ trở thành: Đếm số nghiệm nguyên không âm của phương trình:

1+2+⋯+=x1​+x2​+⋯+xn​=m

Dùng kĩ thuật song ánh, xem rằng giữa mỗi em bé có một số 00 và số kẹo của em bé thứ i nhận được sẽ biểu diễn bằng một dãy gồm xi​ số 1,1, thì bài toán biến thành đếm số cấu hình có dạng:

Với m số 11 vàn−1 số 00

Như vậy, thực tế ta đang đếm số cách đặt n−1 số 00 vào một dãy gồm m+n−1 vị trí, còn lại sẽ là các số 11. Theo quy tắc tổ hợp không lặp, số nghiệm của bài toán sẽ là:

Cm+n−1n−1​

Tuy nhiên, khi lập trình các bạn có thể cần lưu ý cả tới giới hạn dữ liệu của bài toán. nếu bài toán yêu cầu đưa ra kết quả là phần dư sau khi chia cho một giá trị nào đấy thì cần dùng các phương pháp phù hợp như Nghịch đảo modulo, Thuật toán bình phương và nhân hay Phép nhân Ấn Độ tương ứng. Lập trình ở bước này không khó nên tôi sẽ không viết lại code nữa!

Nếu các em bé đều phải nhận được ít nhất 1 chiếc kẹo?

Bài toán có khả năng lắt léo hơn một tí, nếu đề bài đòi hỏi rằng khi chia kẹo, mỗi em bé đều phải được nhận ít nhất 11 chiếc kẹo. khi đó, bài toán sẽ trở thành: Đếm số nghiệm nguyên dương của phương trình:

x1​+x2​+⋯+xn​=m

đối với bài toán này, ta giải như sau: Đặt yi​=xi​−1;∀i:1≤i≤n. lúc đó ta có:

(1)y1​+y2​+⋯+yn​=x1​+x2​+⋯+xn​−n=m−n (1)

Lúc này phương trình xuất hiện hai trường hợp kết quả:

• Nếu như m<n thì phương trình vô nghiệm.
• Nếu m≤n thì bài toán lại trở thành dạng giống với bài toán căn bản, lúc này số nghiệm của phương trình chính là số bộ giá trị(y1​,y2​,…,yn​) thỏa mãn phương trình (1),(1), đấy là:Cm−1n−1​

Phát triển bài toán tổng quát

Các bài toán có dạng như hai bài toán nói trên đều có khả năng phát biểu thành dạng tổng quát như sau: Đếm số nghiệm nguyên của phương trình x1​+x2​+⋯+xn​=m; với xi​≥ai​ (∀i:1≤i≤n).

Lời giải của bài toán này tương tự với bài toán số 2, ta gọi yi​=xi​−ai​;∀i:1≤i≤n và s=∑i=1n​ai​. Phương trình đã cho sẽ trở thành:

(2)y1​+y2​+⋯+yn​=(x1​−a1​)+(x2​−a2​)+⋯+(xn​−an​)=m−s (2)

Giờ ta cần xét tới ba hoàn cảnh kết quả:

• Nếu m<s, thì phương trình đã cho sẽ vô nghiệm.
• Nếu như m=s, thì phương trình đã cho có độc nhất một nghiệm là xi​=ai​;∀i:1≤i≤n.
• Nếu m>s, thì ta cần đếm số bộ thành quả (y1​,y2​,…,yn​) thỏa mãn phương trình (2),(2), đấy là:Cm+n−s−1n−1​

Bây giờ chúng ta hãy cùng xét một số bài toán ứng dụng của công thức chia kẹo Euler trong lập trình thi đấu, để hiểu rõ hơn về phần mềm của bí quyết này trong các kì thi lập trình!

Một số bài toán minh họa

Đếm đường đi

Đề bài

Cho một lưới gồm các ô vuông. Các ô được đánh số từ 00 đến m theo chiều từ trái sang phía phải và từ 00 đến n theo chiều từ dưới lên trên. Giả sử ta đang ở ô (0,0);(0,0); ta chỉ có thể di chuyển trên cạnh các ô vuông theo chiều từ trái sang phía phải hoặc từ dưới lên trên.

Yêu cầu: Hãy tính số đường đi không giống nhau từ ô (0,0)(0,0) đến ô (m,n) của lưới ô vuông?

Input:

• Một dòng độc nhất chứa hai số nguyên m và n.

Ràng buộc:

• 1≤m,n≤5000.
• m+n≤5000.

Output:

• In ra số dư của kết quả của bài toán một khi chia cho 109+7109+7.

Sample Input:

10

Ý tưởng

Nhận xét thấy, một đường đi thỏa mãn gồm m+n bước đi (mỗi bước đi là một cạnh ô vuông). Tại mỗi bước đi chỉ được chọn một trong hai giá trị đi lên (ta đặt là 11) hoặc đi sang phải (ta đặt là 00). Số bước đi lên đúng bằng n và số bước sang phải đúng bằng m. Bài toán lúc này dẫn đến việc tìm coi có bao nhiêu dãy nhị phân có độ dài m+n trong đó có đúng n thành phần có giá trị bằng 11.

Dựa trên bài toán chia kẹo Euler, kết quả cần tìm lúc này là (mm+n​).

Ta có khả năng tính tổ hợp (kn​) bằng quy hoạch động dựa trên tính chất sau của tổ hợp:

(kn​)=(k−1n−1​)+(kn−1​)

Độ phức tạp: O(n2). Các bạn cần liên kết với việc tính toán modulo liên tục để tránh gây ra tràn số nếu sử dụng ngôn ngữ C++.

Thiết lập

1
2 2

Sample Output:

#include 
#define int long long 

using namespace std;

const int MOD = 1e9 + 7;

void pre_compute(vector < vector < int > > &ncr, int max_size)
{
    ncr = vector < vector < int > >(max_size + 1, vector < int >(max_size + 1));

    for (int i = 0; i <= max_size; ++i)
    {

Tổng kết

Và đó là tổng hợp về bài toán chia kẹo Euler do Học May tổng hợp. Cảm ơn các bạn đã đọc, hi vọng rằng bài viết của chúng tôi sẽ giúp ích cho bạn. Hẹn gặp lại bạn trong những bài viết sắp tới nhé.