Công thức xác suất là một trong những kiến thức quan trọng trong chương trình học tập toán học. Việc học hiểu công thức và biết cách áp dụng công thức xác suất để làm bài tập là 1 trong những điều quan trọng đối với học sinh. Hôm nay hocmay.vn sẽ cung cấp cho bạn đầy đủ các kiến thức về công thức xác suất để bạn có thể làm quen cũng như hiểu cách làm và cách áp dụng đối với công thức này.
Công thức tính tổ hợp
Dưới đây là các công thức tính tổ hợp:
Tổ hợp lặp
Cho một tập hợp A gồm n phần tử và một tập hợp B gồm k phần tử, với k là một số tự nhiên bất kỳ. Một tổ hợp lặp chập k của n phần tử là một tập hợp gồm k phần tử, trong đó mỗi phần tử có thể được lựa chọn từ n phần tử của tập A.
Số tổ hợp lặp chập k của n phần tử có thể tính bằng công thức sau:
Công thức tổ hợp lặp:
C(k, n) = C(n + k – 1, k) = C(n + k – 1, n)
Tổ hợp không lặp
Cho một tập hợp A gồm n phần tử. Một tập con gồm k phần tử của tập A (với 1 ≤ k ≤ n) được gọi là một tổ hợp chập k của n phần tử.
Số tổ hợp chập k của n phần tử có thể tính bằng công thức sau:
Công thức tổ hợp không lặp:
C(k, n) = A(k, n) / (k!)
Trong đó A(k, n) là số hoán vị chập k của n phần tử, và k! là giai thừa của k.
Quy ước:
C(0, n) = 1
Tính chất:
- C(0, n) = C(n, n) = 1
- C(k, n) = C(n – k, n)
- C(k, n) = C(k – 1, n – 1) + C(k, n – 1)
- C(k, n) = (n – k + 1) / k * C(k – 1, n – 1)
Công thức xác suất

Sau đây là công thức xác suất của một biến cố là:
Với :
- P(A) là xác suất của sự kiện A
- n(A) là số kết quả thuận lợi
- n(S) là tổng số sự kiện trong không gian mẫu
Chú ý: Số kết quả thuận lợi là số biến cố mà A có thể xảy ra.
Công thức xác suất căn bản
| Danh sách bí quyết xác suất trong toán học | |
|---|---|
| Phạm vi xác suất | 0 ≤ P(A) ≤ 1 |
| Bí quyết cộng xác suất | P(A∪B) = P(A) + P(B) – P(A∩B) |
| Biến cố đối | P(A’) + P(A) = 1 |
| Biến cố độc lập | P(A∩B) = 0 |
| Công thức độc lập | P(A∩B) = P(A) ⋅ P(B) |
| Công thức xác suất có điều kiện | P(A | B) = P(A∩B) / P(B) |
| Công thức Bayes | P(A | B) = P(B | A) ⋅ P(A) / P(B) |
Ví dụ minh họa công thức xác suất
VD 1: Xác suất để rút một lá bài từ bộ bài chuẩn mực 52 quân là quân Át
Giải
không gian mẫu n(S)=52
Số quân bài Át trong bộ bài là: 4. Vì điều đó có 4 năng lực xảy ra=> n(A)=4
Gọi P(A) là xác suất rút ngẫu nhiên được 1 quân Át
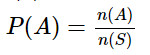
VD 2: Tính xác suất khi xúc con xúc sắc nhận được mặt lẻ chấm.
Giải
Không gian mẫu: n(S)=1,2,3,4,5,6
Số kết quả thuận lợi của A là: n(A)=1,3,5
Gọi P(A) là xác suất nhận được mặt lẻ chấm
P(A)=3/6=0.5
Các dạng bài tập áp dụng công thức xác suất
Dạng 1: Tính xác suất của biến cố xung khắc và biến cố đối
Phương pháp giải:
- Đầu tiên, xác định phép thử T và tính số phần tử trong không gian mẫu |Ω|.
- Xác định biến cố A và từ đó suy ra biến cố A đối (¬A).
- Tính số phần tử của tập mô tả biến cố đối |Ω¬A| và tính xác suất P(¬A) = |Ω¬A| / |Ω|.
- Tính xác suất của biến cố A là P(A) = 1 – P(¬A).
- Xác định biến cố xung khắc nếu cần.
Ví dụ minh họa:
Ví dụ 1: Trong một hộp gồm 20 viên bi, có 12 viên bi màu xanh và 8 viên bi màu vàng. Lấy ngẫu nhiên 3 viên bi ra khỏi hộp. Tính xác suất:
a) Lấy được ít nhất một viên bi màu vàng.
b) Lấy được đủ 2 màu.
Lời giải:
a) Gọi A là biến cố “Lấy ít nhất một viên bi màu vàng.”
Bước 1: |Ω| = C(3, 20) (số cách lấy 3 viên từ 20 viên bi)
Bước 2: ¬A là biến cố “Không lấy viên bi màu vàng,” |Ω¬A| = C(3, 12) (số cách lấy 3 viên từ 12 viên bi xanh)
Bước 3: Tính P(¬A) = |Ω¬A| / |Ω| = C(3, 12) / C(3, 20).
Bước 4: Tính P(A) = 1 – P(¬A).
a) Gọi B là biến cố “Lấy được 1 viên bi xanh và 2 viên bi vàng.”
C là biến cố “Lấy được 2 viên bi xanh và 1 viên bi vàng.”
Bước 5: Tính P(B ∪ C) = P(B) + P(C) (vì B và C là xung khắc).
P(B) = |B| / |Ω| = C(1, 12) * C(2, 8) / C(3, 20)
P(C) = |C| / |Ω| = C(2, 12) * C(1, 8) / C(3, 20)
Tính tổng để có P(B ∪ C).
Dạng 2: Tính xác suất sử dụng công thức cộng và nhân
Phương pháp giải:
- Xác định biến cố của các xác suất, có thể đặt tên cho các biến cố A, B, C, D…
- Tìm mối quan hệ giữa các biến cố và biểu diễn biến cố trung gian.
- Sử dụng các mối quan hệ để chọn công thức cộng hoặc công thức nhân phù hợp.
Ví dụ minh họa:
Ví dụ 1: Gieo một con súc sắc 3 lần liên tiếp. Tính xác suất để:
a) Xuất hiện mặt 6 chấm trong cả ba lần.
b) Xuất hiện các mặt có số chấm giống nhau.
c) Xuất hiện mặt 3 chấm ít nhất 1 lần.
Lời giải:
a) Xác suất để mỗi lần súc sắc xuất hiện mặt 6 chấm là 1/6. Vì các lần súc sắc là độc lập, nên xác suất để cả ba lần đều xuất hiện mặt 6 chấm là (1/6)^3.
b) Để tính xác suất xuất hiện các mặt có số chấm giống nhau, chúng ta có thể tính xác suất ngược lại (xác suất không xuất hiện các mặt giống nhau) và trừ đi từ 1. Xác suất ngược lại là tổng của xác suất không có mặt giống nhau, có đúng 1 mặt giống nhau và có đúng 2 mặt giống nhau.
c) Để tính xác suất xuất hiện mặt 3 chấm ít nhất 1 lần, chúng ta có thể tính xác suất ngược lại (xác suất không xuất hiện mặt 3 chấm trong cả ba lần) và trừ đi từ 1. Xác suất ngược lại là (5/6)^3.
Tổng kết
Bài viết trên Học May đã cung cấp cho bạn đầy đủ các kiến thức về công thức xác suất và các dạng bài tập. Hi vọng bài viết trên có thể hỗ trợ bạn tham khảo và áp dụng thành công công thức xác suất. Hãy cùng chúng tôi tìm hiểu thêm nhiều thông tin hữu ích khác nữa nhé!










